프랙탈과 코흐 눈송이의 수학적 특성과 의미
여러분은 자연 속에서 눈에 보이는 패턴이 수학과 깊은 관련이 있다는 사실을 알고 있나요? 오늘은 ‘프랙탈’이라는 흥미로운 개념과 대표적인 프랙탈 도형인 ‘코흐 눈송이’에 대해 알아보려고 합니다. 눈에 보이는 간단한 도형이지만, 수학적으로 보면 무한에 가까운 신비로운 성질을 가지고 있죠. 이 글을 통해 프랙탈이란 무엇인지, 코흐 눈송이가 어떻게 만들어졌는지, 그리고 수학적으로 어떤 의미가 있는지 하나씩 알아보아요.
목차
- 프랙탈이란
- 코흐 눈송이란?
- 코흐 눈송이의 특성과 수학적 의미
1) 무한한 길이
2) 자기유사성
3) 면적의 수렴 - 마무리
프랙탈이란?
프랙탈(fractal)은 1970년대 수학자 브누아 망델브로(Benoît Mandelbrot)가 본격적으로 정의한 개념이에요. 프랙탈이란 전체와 부분이 유사한 형태를 반복적으로 가지는 도형을 의미해요. 쉽게 말하면, 프랙탈 도형은 작은 조각 하나를 보더라도 큰 전체 도형과 비슷한 모양을 가지고 있다는 거죠. 이러한 성질을 **자기 유사성(self-similarity)**이라고 해요.
자연 속에서는 나무의 가지, 구름, 해안선, 산의 윤곽 등에서 프랙탈 형태를 자주 볼 수 있어요. 여러분이 해변에서 모래성 쌓기를 할 때 해안선을 보면서 “이 선은 왜 이렇게 구불구불하지?”라고 생각한 적이 있나요? 그 구불구불한 해안선은 작은 부분을 확대해도 큰 모습과 비슷한 형태를 유지하는 프랙탈 성질을 가진답니다.
코흐 눈송이란?
프랙탈의 대표적인 예로, 1904년 스웨덴의 수학자 헬게 폰 코흐(Helge von Koch)가 만든 코흐 곡선(Koch curve)을 들 수 있어요. 코흐 곡선은 한 직선을 시작으로 그 선을 무한히 반복해서 분할하며 만들 수 있는 프랙탈 도형이에요.
코흐 곡선은 다음과 같이 생성됩니다:
1. 먼저 한 선분을 준비해요.
2. 그 선분의 중간을 삼등분한 다음, 중간 부분을 삼각형 모양으로 바깥쪽으로 올려서 새로운 "갈매기 날개" 모양을 만들어요.
3. 이렇게 분할한 선분 하나하나를 동일한 방식으로 계속 나누는 거예요.
코흐 눈송이(Koch snowflake)는 코흐 곡선을 세 개 이어 붙여서 삼각형 모양으로 만든 도형이에요. 이 도형은 단순한 삼각형에서 출발하지만, 무한히 계속된 분할로 인해 눈송이처럼 아름다운 프랙탈 모양을 가지게 돼요.

코흐 눈송이의 특성과 수학적 의미
1) 무한한 길이
코흐 눈송이는 겉으로는 유한한 크기를 가지고 있는 것처럼 보이지만, 그 둘레 길이는 무한해요. 선분을 계속해서 나누고 삼각형 모양을 추가하는 과정에서 전체 둘레 길이는 점점 늘어나며, 결국 무한한 길이가 됩니다. 유한한 면적을 가지면서도 둘레는 무한대인 도형이 탄생하게 되는 거죠.
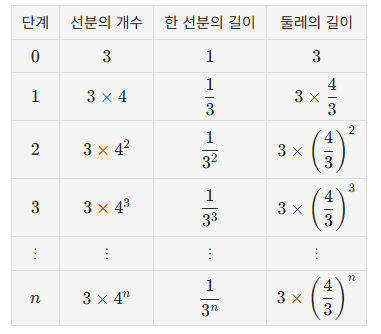
2) 자기 유사성
앞서 말한 자기 유사성 개념에 따라, 코흐 눈송이의 각 작은 부분도 전체 모양과 비슷하게 생겼어요. 눈송이를 확대해보면 작은 삼각형들이 계속 반복되며 나타나는 걸 볼 수 있어요. 이 점에서 코흐 눈송이는 프랙탈의 대표적인 예시라고 할 수 있습니다.

3) 면적의 수렴
코흐 눈송이의 면적은 유한하지만 둘레는 무한히 길어진다고 했죠. 이는 무한한 반복 속에서도 도형의 면적은 점점 일정한 값으로 수렴한다는 걸 의미해요. 수학적으로 보면 코흐 눈송이의 면적은 초기에 출발한 삼각형의 약 1.6배에 가까운 값으로 수렴하게 됩니다. 이는 무한한 반복 속에서도 도형이 차지하는 공간이 유한하다는 흥미로운 사실을 보여줍니다.


마무리
코흐 눈송이와 같은 프랙탈은 자연 현상을 설명하는 데 유용해요. 예를 들어, 해안선의 길이나 산의 윤곽선 등을 수학적으로 계산할 때 프랙탈 개념을 적용할 수 있어요. 또한 프랙탈 이론은 컴퓨터 그래픽, 예술, 데이터 압축 기술 등 다양한 분야에 활용되고 있답니다.
특히 컴퓨터 그래픽에서는 프랙탈을 이용해 자연의 풍경을 더 사실적으로 구현할 수 있어요. 나무의 가지 모양이나 구름의 형태를 프랙탈 알고리즘을 통해 표현하면 자연스러운 모양을 쉽게 얻을 수 있습니다.
여러분도 직접 코흐 눈송이를 만들어 볼 수 있어요. 종이와 자를 준비한 후, 선을 그려서 위의 단계를 따라가며 선분을 계속 나누어 보세요. 반복하는 과정에서 도형이 점점 복잡해지고 눈송이 같은 아름다운 모양을 갖추는 걸 볼 수 있을 거예요.
또는 컴퓨터 프로그래밍을 통해 코흐 눈송이를 구현해볼 수도 있어요. 파이썬 같은 프로그래밍 언어에서는 간단한 코드로 코흐 눈송이를 그릴 수 있습니다. 이는 여러분이 수학과 컴퓨터 과학을 결합해 도형을 생성하는 흥미로운 경험이 될 거예요.
프랙탈과 코흐 눈송이는 수학적으로도 아름답지만, 자연과 우리가 사는 세상 속 패턴을 이해하는 데 중요한 도구가 되기도 합니다. 단순한 반복으로 무한히 복잡하고 아름다운 도형을 만들어가는 프랙탈의 세계, 흥미롭지 않나요? 이제 여러분도 자연 속에서 프랙탈을 찾아보고, 무한과 자기 유사성의 세계에 빠져보세요!
