오랜만에 영재 수업 준비...
원래 원정 수업(?)은 조금 시큰둥 했으나..
여차여차 해서 아시는 분의 부탁을 받아 간만에 영재수업 지도를 부탁받게 되었다.
일단 수학체험학습이든, 영재학습이든
교육과정과 연계되지 않은 단순 흥미 위주의 주제는 조금 마음에 들지 않아서
최대한 교육과정과 연계하여
'소수'의 중요성을 이야기할 수 있는 주제로 유한군의 성질을 선택해보았다.
아마도 임용공부를 했던... 정수론과 현대대수학 내용을 바탕으로 수업의 흐름을 간단히 소개할까 한다.
일단 해당 주제를 선택한 이유는...
'내가 재미있어 하는 부분이여서 ㅋㅋㅋ'
대학생 때 전공과 관련된 블로그를 조금 운영하기도 했었는데 ㅋㅋㅋ
일단 수업의 큰 흐름을 적어보고 혹시라도 영재수업을 고민하시는 분이 있다면
참고하고.. 더 좋은 자료와 수업이 되길 기대하며...
(학습지를 별로 꾸미고 싶지 않아서 ㅋㅋ 더 예쁘게 참고해서 각자 만들어보세요)
흐름(중1 기준)

거듭제곱 문제 - 이번 수업을 이해하면 풀 수 있을거야 ㅋㅋㅋㅋ
이번 수업의 목표와도 같은 문제
도입 - 시계에서의 덧셈
간단한 퀴즈를 통해 합동식을 직관적으로 이해해보자
수학 역사 소개
기존에 쓰고 있던 연산(덧셈, 곱셈) 등을 형식적으로 정의하기 시작
따라서 우리는 '연산'이라는 용어를 수학적으로 정의할 필요가 있다
수리철학의 흐름 정도를 이야기 해주면 좋을 듯
용어 정의
집합: 수들의 모임 정도로 간단하게 (교육과정 고1)
원소: 그 안에 들어있는 수
이항연산: 2개의 수를 대입하여 새로운 수를 만들어내는 함수 관계, 약속
닫혀있다: 직관적으로..
항등원 + 역원: 덧셈과 곱셈의 예를 들어 예시 위주로 소개
합동식은 나중에 설명

연습해보기 Z4
- 수로 연산표 만들기
- 문자로 연산표 만들기
-> 두 연산표의 구조가 같음을 표를 변형해서 확인해보기
-> 문자에서 d가 항등원이라 순서를 바꾸면 같은 모양이 나옴
군의 정의 적용해보기(여러가지 집합과 연산에서 군이 성립하는지)

합동식 소개하기...
원소가 유한개인 군의 연산을 표현하기 위해서 합동식을 설명
수학에서의 합동이라는 이미지로 합동식을 도입
+ 실제로 유리수에서 약분을 통해 같다라고 쓰는 부분도 합동식과 비슷하다고 소개
곱셈의 연산표를 만들어보고 곱셈은 군이되는지 질문
법 5에서 0으로 계산하는 나오는 줄을 지우고 군이되는지 질문 -> 소수일 때는 0 제외하면 곱셈군이 됨
법 6에서 0이 나오는 줄을 지우고 군이되는지 질문 -> 소수가 아닐 때는 0인자가 있어서 군이 되지 않음

1번표는 앞서 법 5의 곱셈 연산에서 0을 제외하고 옮겨오고
2번표는 1을 e로... 2를 a로... 변환만(세로줄 오타 ㅋㅋ)
구조를 비교하고 3번표에서 c와 b의 위치를 바꾸어 연산표를 만들기
4번표에서 e를 0으로, a를 1로, c를 2로, b를 3으로 바꾸면 덧셈과 동형 완성
즉 연산의 규칙과 원소의 계산 결과는 달랐지만 두 연산은 구조적으로 같음을 소개 => 동형성에 대한 이해

합동식이 없더라도 대부분의 규칙은 아이들이 알고 있을듯?
11의 배수의 규칙을 법 11에서 찾아보는 활동이 주가 됨 -> 플러스 마이너스 반복해서 11의 배수가 되면 된다
유한군의 성질
용어 소개 - 위수
증명은 수학적으로 가능하지만 매우 어렵고 몰라도 된다. ㅋㅋ
원소의 위수를 시계의 덧셈에서 소개하며
2, 3, 5 등의 위수를 확인해보며 직관적으로 원소들의 위수가 군의 위수의 약수가 된다는 사실은 확인하고 넘어가야 함
생성원이라는 것은 모든 원소를 만들어내는 원소,
어떤 녀석들이 생성원이 될까? -> 유한군의 위수와 서로소인 원소들

법 2와 법 3의 생성원의 조합이 법6의 생성원이 될 수 있음을 소개
소수일 때는 생성원의 개수가 항등원을 제외하면 되므로 p-1임을 소개
법 6의 생성원의 개수는 법2와 법3의 생성원의 개수의 곱으로 구할 수 있음을 소개
그럼 세 소수의 곱(법 30)일 때 생성원의 개수는?
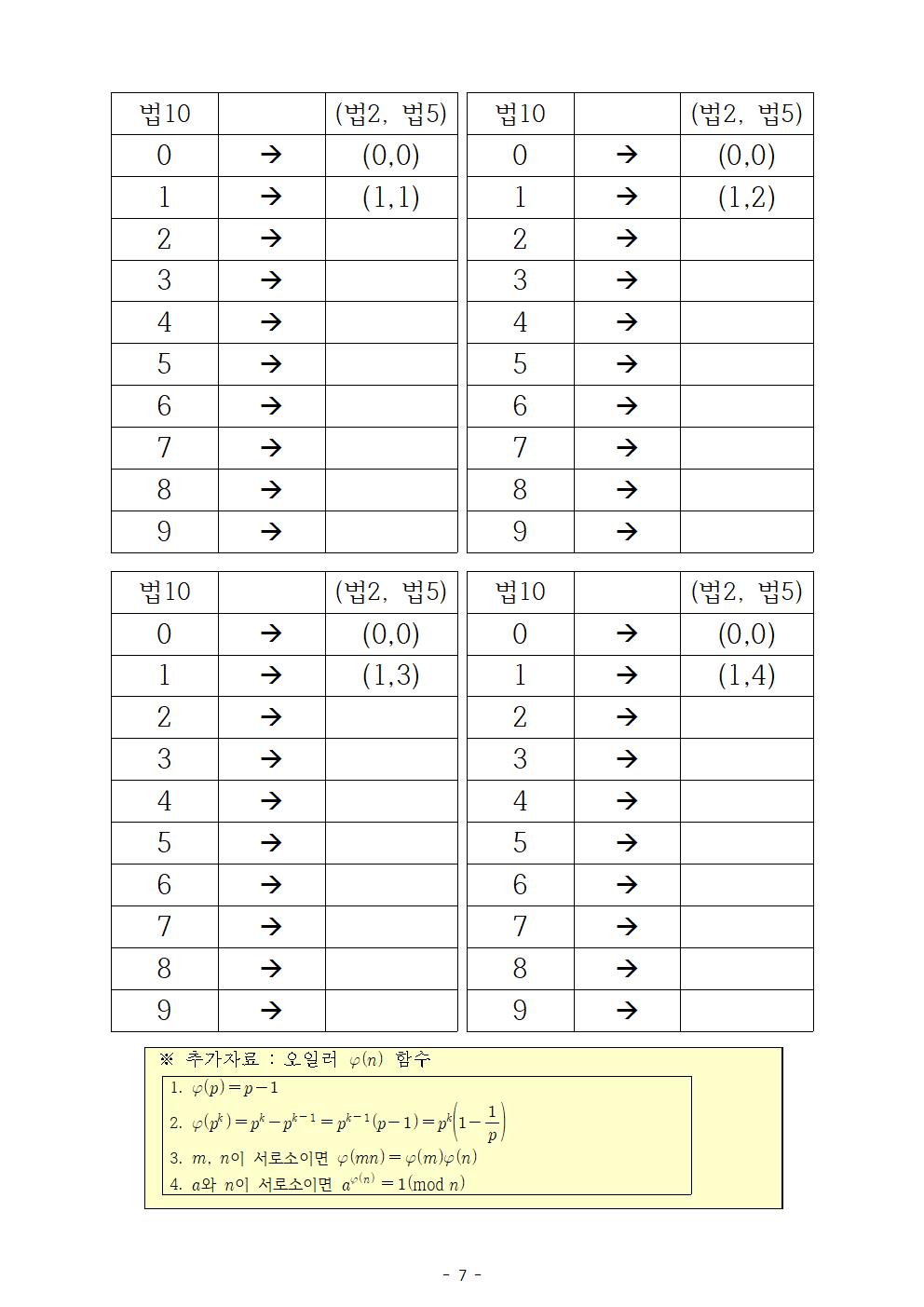
오일러 함수는 생성원의 개수를 구하는 함수임을 소개
결국 서로소인 원소의 개수임
피의 케이제곱일때는 그냥 칠판에서 간단히 소개함
5^3의 서로소인 개수는... 5의 배수들을 제외하면 되므로 5의 배수가 몇개가 나오는지 발문하면 금방 대답함
그럼 오늘 수업을 총 아우르는 오일러 함수의 성질 소개(4번)
덧셈의 유한군에서 서로소인 녀석들만 가지고 곱셈군을 만들 수 있었다
그리고 이 곱셈군의 위수는 오일러함수로 구할 수 있다.
그리고 각 원소의 위수는 모르지만 군의 위수만큼 연산하면 항등원이 나온다.
그래서 이 합동식을 가지고 맨 처음 주어진 계산식을 구하면 된다!!!

오늘 수업을 통해 소수를 연구하는 것의 중요성
소인수분해가 왜 중요한지... 등을 소개해줄수 있다.
마지막으로 Z12의 곱셈 연산표를 만들어보고
0인자를 제외해 군을 만들고..
그 군이 Z4와 동형인지 확인해보며...
원소의 위수가 최대 2인것을 확인해 동형이 아닌 것을 언급해주고
유한생성가환군의 정리 살짝 언급해주고 수업 끝
수업반성]
3시간 분량의 수업이었지만... 조금 똘똘한 학생들이면 2시간 정도면 해결 가능
교사의 안내가 수시로 필요하다보니... 힘들다 ㅋㅋㅋ
학생들이 길게 몰두하며 해결할 수 있는 과제가 없었다.
수학에 흥미가 없는 학생이라면 과제를 매우 어려워한다 ㅋㅋ
새로운 용어들이 많아 있어보인다
조금 더 수정 보완이 필요하며 학습지를 예쁘게 꾸밀 필요가 있다 ㅋㅋㅋㅋ
** 수업과 관련된 좋은 아이디어 있으면 댓글 부탁드려요!
'공부하는 > 육아, 수학, 교육' 카테고리의 다른 글
| 갤럭시탭 S7 사전예약 가격 정보, 예약 판매 사은품 및 할인 정보 (258) | 2020.08.18 |
|---|---|
| 갤럭시 탭... wifi모델, LTE모델... 어떤 걸 써야할까요? (LTE 데이터 쉐어링) (144) | 2020.08.13 |
| 갤럭시탭 S7, S6, S6 Lite 사양 비교 (구매전 알아봐야 할 것들) (2110) | 2020.08.10 |
| [수학] 소용돌이 모양의 사각형 딱지! (curlicue square, curlicue fractal) (1) | 2020.06.10 |
| 정팔각형 만들기와 전통 노리개 만들기 (by통통한딸기) (267) | 2020.05.06 |




댓글